Aportes de los egipcios y babilonios a las matemáticas

Uno de los primeros indicios del uso de las matemáticas por parte de la humanidad, más allá de simplemente contar, proviene de los egipcios y los babilonios.
Ambas civilizaciones desarrollaron sistemas matemáticos que, aunque se parecían en algunos aspectos, también presentaban diferencias. Hoy en día, sus aportes se estudian en las clases de matemáticas como parte de la historia del pensamiento numérico.

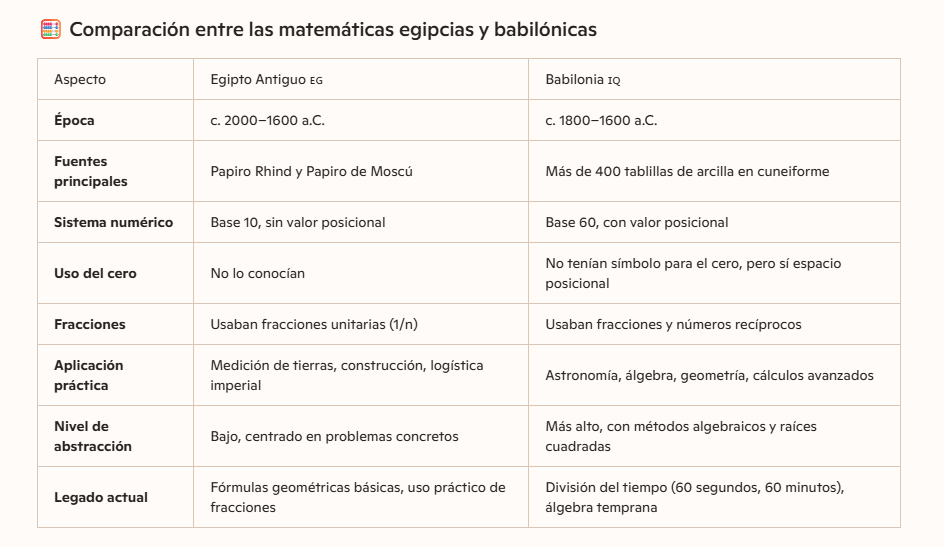
En el caso de los egipcios, aunque dejaron jeroglíficos por todos lados, lo que más nos dice sobre sus matemáticas son dos papiros: el de Ahmes y el de Moscú.
Estos documentos, que datan de mil años antes de que los griegos empezaran a filosofar, contienen problemas matemáticos con sus soluciones. Eran como cuadernillos de ejercicios para estudiantes jóvenes, enfocados en lo que hoy llamaríamos aritmética aplicada.

A través de esos papiros vemos qué tipo de problemas les interesaban a los egipcios: asuntos prácticos, como alimentar a un ejército o calcular raciones para los obreros. Lo que no vemos es la intención de formular principios matemáticos generales o teorías abstractas.

Por otro lado, las matemáticas babilónicas, aunque también estaban al servicio del Estado, eran más sofisticadas en muchos aspectos.

Aunque hay evidencia de estudios astronómicos más profundos en épocas helenísticas, los registros más antiguos muestran un enfoque muy práctico. Aun así, su sistema de conteo era posicional, lo que fue un palo. De hecho, el matemático Otto Neugebauer lo consideró uno de los mayores inventos de la humanidad.

Ese sistema les permitió escribir números enormes con facilidad y realizar una gama más amplia de cálculos. También hay evidencia de que usaban tablas de interpolación para resolver ecuaciones no lineales y hasta tenían un método elegante para calcular la raíz cuadrada de 2.

El contraste con los griegos es claro: mientras los egipcios y babilonios se enfocaban en resolver problemas concretos, los griegos optaron por la vía de las matemáticas abstractas, en especial la geometría. Ese modelo griego se convirtió en el estándar de las matemáticas hasta tiempos modernos.

Los mejores profesores disponibles

Vamos

¿Qué aportó Egipto a las matemáticas?

Los egipcios jugaron un papel clave en el desarrollo de las matemáticas tal como las conocemos hoy. Muchos de sus conocimientos pasaron a los griegos, quienes los usaron como base para desarrollar su propio sistema matemático.
Para compensar las limitaciones de su sistema numérico, idearon métodos ingeniosos para multiplicar y dividir, como se muestra en el papiro Rhind. Aunque lo que sabemos sobre las matemáticas egipcias es limitado, hay evidencia suficiente para demostrar que eran muy buenos para resolver problemas prácticos.

👉🏽 De seguro te va a interesar leer sobre: Influencia de la India y China en las matemáticas.

• 📜 Los papiros de Ahmes (Rhind) y Moscú: estos documentos antiguos contienen problemas de aritmética y geometría con sus soluciones. Fueron escritos como guías educativas para jóvenes estudiantes y muestran que los egipcios usaban un sistema decimal, aunque no posicional. Eso significa que no necesitaban un símbolo para el cero, como en el sistema romano.

• ➕➖ Sumaban y restaban sin problema, pero para multiplicar o dividir tenían que usar métodos más lentos, como duplicar o reducir a la mitad—algo parecido a cómo funciona un sistema binario.

• 🧠 Método de prueba y error: los egipcios no buscaban fórmulas abstractas ni relaciones complejas entre números. Usaban técnicas de ensayo y error para resolver problemas y sus fórmulas les permitían estimar áreas y volúmenes con suficiente precisión para sus necesidades.

• 📐 Álgebra básica y ecuaciones: sabían resolver ecuaciones lineales y algunas cuadráticas simples mediante conjeturas y fuerza bruta, un método que se siguió empleando durante siglos.

• 📄 Fracciones unitarias: en el papiro Rhind, que tiene 87 problemas, se ve que los egipcios preferían usar fracciones como 1/2, 1/4, 1/8, en vez de fracciones más complejas como 2/5 o 7/16.
  Por ejemplo, escribían 3/4 como 1/2 + 1/4 y 4/5 como 1/2 + 1/4 + 1/20. Aunque parecía complicado, era fácil de manejar una vez que te acostumbrabas.

• 🏛️ El papiro de Moscú: con 25 problemas, este muestra cómo calcular el volumen de una pirámide truncada y el área de una media esfera.

• 📏 Sistema de medición: los egipcios usaban el codo como unidad de medida (unos 52.3 cm) y medían con reglas y cuerdas con nudos. Estas técnicas se emplearon en la construcción de las pirámides y de otros monumentos.

• 🍞 Problemas con fracciones: muchos ejercicios del papiro Rhind trataban sobre cómo dividir n panes entre 10 hombres, usando fracciones. De hecho, 81 de los 87 problemas involucran operaciones con fracciones.

• 🧮 Pensamiento práctico, no abstracto: a diferencia de los griegos, que consideraban los números como ideas abstractas, los egipcios los veían como colecciones reales de objetos.
  Por ejemplo, si hablaban del número 8, pensaban en 8 cosas específicas, no en el concepto de “ocho” como tal.

¿Qué aportes hicieron los babilonios a las matemáticas?

Las matemáticas babilónicas se desarrollaron en Mesopotamia, desde los tiempos de los primeros sumerios hasta la caída de Babilonia en el año 539 a.C. Son especialmente conocidas por su sistema numérico único, que aún influye en la medición del tiempo y de los ángulos hoy en día.

 👉🏽 De seguro te va a interesar leer sobre: Aportaciones de los Mayas a las Matemáticas.

La región fértil entre los ríos Tigris y Éufrates fue clave para que la humanidad pasara de vivir como seminómadas a formar ciudades y centros urbanos. Ese cambio social, junto con la agricultura, permitió a la gente dedicar tiempo a estudiar y a adquirir conocimiento.

Una de las grandes contribuciones de los sumerios y babilonios fue la escritura cuneiforme, que les permitió conservar y transmitir información de generación en generación. Muchas de esas tablillas de arcilla han sido encontradas por arqueólogos y nos dan pistas sobre cómo vivían y pensaban.

Sistema numérico de base 60
Los babilonios usaban un sistema sexagesimal (base 60), diferente del sistema decimal que usamos hoy. A diferencia de los egipcios, griegos y romanos, sí tenían un sistema posicional: los números escritos más a la izquierda valían más, igual que en nuestro sistema moderno.

Para representar los números del 1 al 59, usaban dos símbolos: uno para la unidad y otro para el diez. Por ejemplo, si escribieran el símbolo de 60 seguido del de 23, eso representaría 83.

El número 60 se escribía igual que el número 1, y como no tenían punto decimal, el valor real de cada símbolo se deducía por el contexto.

¿Por qué base 60?
Porque el número 60 tiene muchísimos divisores: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 y 60. Eso lo hacía ideal para cálculos. Hoy seguimos usando ese sistema cuando decimos que hay 60 segundos en un minuto, 60 minutos en una hora y 360 grados en un círculo (60 × 6).

El cero como marcador de posición
Los babilonios también fueron pioneros en el uso de un símbolo para representar el cero, aunque no como número, sino como marcador de posición. Eso les permitió escribir números grandes y hacer cálculos más complejos—algo que ni los egipcios, ni los griegos, ni los romanos tenían en ese momento.

👉🏽 De seguro te va a interesar leer sobre: Culturas antiguas y las Matemáticas.

En resumidas cuentas

Los egipcios y los babilonios pusieron los cimientos de las matemáticas que usamos hoy sin saberlo. Los egipcios, con sus fracciones unitarias, cálculos geométricos y técnicas de medición, contribuyeron a construir monumentos como las pirámides y nos dejaron fórmulas que aún se enseñan. Los babilonios, por su parte, nos legaron el sistema de base 60, que todavía usamos para medir el tiempo (60 segundos, 60 minutos) y los ángulos (360 grados). Aunque sus métodos eran prácticos y no tan abstractos como los de los griegos, su legado perdura en cada reloj, cada plano y cada cálculo que hacemos en la vida diaria.